Las transformaciones isométricas son transformaciones de figuras en el plano que se realizan sin variar las dimensiones y el área de las mismas; la figura inicial y la final son semejantes, y geométricamente congruentes.
La palabra isometría tiene su origen en el griego iso(igual o mismo) y metria (medir), una definición cercana es igual medida. Existen tres tipos de isometrías traslación, simetría y rotación.

Traslación
La traslación es una isometría que realiza un cambio de posición, determinada por un vector.
En la traslacion el vector se encarga de trasladar la figura, la imagen se ubica dependiendo la medida del vector.

Para realizar una traslación sumando 2 o mas vectores, primero se debe realizar la traslación con el primer vector y luego desde la imagen obtenida con el primer vector se traslada con el segundo vector y asi sucesivamente cuando sean mas vectores.

Ejercicio traslación:

Se necesita la figura a trasladar y un vector, en este caso el triangulo ABC y el vector V

Desde cada punto de la figura se aplica el vector

Y finalmente tenemos la figura trasladada

Simetría

Correspondencia exacta en la disposición regular de las partes o puntos de un cuerpo o figura con relación a un centro, un eje o un plano.
Se divide en simetría axial y simetría central.

Simetría axial

La Simetría Axial o de Reflexión mágica es una transformación respecto de un eje de simetría, en la cual cada punto de una figura se asocia a otro punto llamado imagen, que cumple con las siguientes condiciones:
a) La distancia del punto y su imagen al eje de simetría es la misma
b) El segmento que une el punto con su imagen es perpendicular al eje de simetría

Ejercicio de simetría axial:

Ubicamos la figura en el plano cartesiano

Para realizar la simetria respecto al eje Y, tenemos que ubicar cada punto de la figura a la misma distancia cada uno del eje de simetria Y

Para realizar la simetria respecto al eje X, tenemos que ubicar cada punto de la figura a la misma distancia cada uno del eje de simetria X

Simetría central

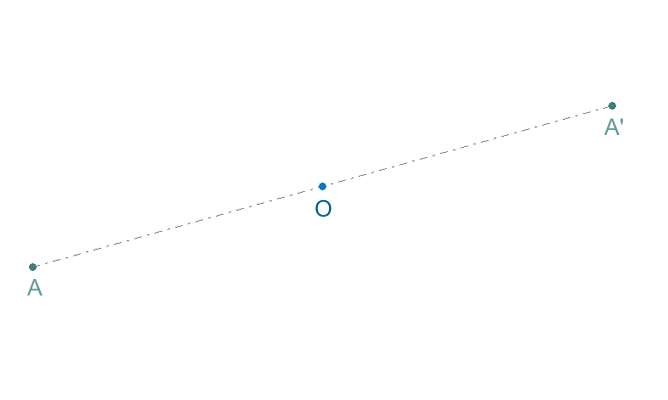
Una simetría central es una transformación en que a cada punto del plano se le asocia otro punto del plano llamado imagen, que debe cumplir con las siguientes condiciones:
a) El punto y su imagen están a igual distancia de un punto llamado centro de simetría.
b) El punto, su imagen y el centro de simetría pertenecen a una misma recta.

Ejercicio simetria central:

Necesitamos tener ubicada la figura y un punto central

Luego trazamos una linea desde cada punto al centro, esta linea debe seguir hasta el otro lado, sobresaliendo la misma distancia que hay entre los puntos de la figura y el punto centro

Rotación



Una rotación es un movimiento en el plano de cambio de orientación de un cuerpo, de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante de un punto fijo y que tiene las siguientes características:
Un punto denominado centro de rotación.
Un ángulo
Un sentido de rotación.



















Ejercicio de rotacion:


Necesitamos la figura que deseamos rotar, un punto que se llama centro de rotacion y el angulo de giro





Debemos trazar una linea desde el centro de rotacion hasta el punto A, luego calculamos en este caso un angulo de 45º sobre la linea OA, despues sobre la linea obtenida a los 45º medimos la misma distancia que hay en la linea OA y ubicamos el punto A`





Repetimos el proceso pero ahora con el punto C y obtendremos C`





Realizamos el mismo proceso pero ahora con el punto B y obtendremos B`
Nota: El orden puede ser a su gusto





Finalmente se unen todos los puntos obtenidos y tendremos una figura rotada en 45º.